Could Meeting the Process Capability (Cpk) Spec Lead to Lot Rejection?
Some companies have decided to require their suppliers to only ship lots to them if the process capability index Cpk ≥ 1.33 (4-sigma), or Cpk ≥ 1.67 (5-sigma). This tactic is designed to provide some assurance that the vast majority of material received conforms to the buyer’s specifications. The ultimate goal of which would be to achieve Cpk ≥ 2.00 (i.e., 6-sigma process capability).
However, before you make any lot accept/reject decision based on the Cpk value reported by the supplier, or before you attempt to verify the supplier’s numbers by repeating the test, you will need the following contextual information:
- Sequence of Production
- Process Stability
- Sub-Grouping Method
- Sample Size
- Manufacturing Process, Equipment, and Parameters
- Inspection Methods
(You can read more about each of these elements in my last post here)
The point is that if you, as a buyer, decide to impose a capability requirement, then you better know everything about how your supplier is performing the analysis, or it may be pretty much meaningless.
By way of illustration lets take an example of a case that on the surface seems to be pretty straightforward. Suppose the supplier inspects all the units in a lot of size 1000 (hence there is no sampling error for the supplier) and gets a Cpk = 1.33, and in addition, the buyer's and supplier's measurement systems are in perfect agreement. Now suppose that at the buyer's incoming inspection they check a random sample of 10 units from the lot to confirm the Cpk ≥ 1.33 requirement has been met. Well surprise, surprise because about 50% of the time the buyer will reject the shipment.
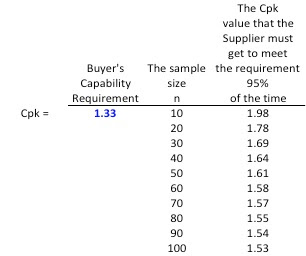
Table 1: Buyer's Requirement is a Cpk of 1.33
How can this happen when we were so careful? Well, suppose you flip a coin 10 times, how many heads would you expect to see? Since the probability of getting head is .5, we would expect to see 5 heads.
Now try this little experiment for yourself. Sometimes you will see more than 5 heads, sometimes less, and sometimes 5. So there is an interval around the expected value (5), where other outcomes may occur with a certain probability, which depends of the variability of the statistic. This is called the confidence interval.
In other words, if you as a buyer, randomly sample and measure 30 parts from a process that has a supplier-reported Cpk of 1.33, you are likely to get a range of process capability values from 0.97 to 1.69, with the average being near 1.3.
So to be 95% confidence of lot acceptance by the buyer, assuming the buyer will sample 30 parts, the supplier will need to achieve a Cpk of 1.69. (See Table 1 below).
The two tables below show the Cpk number the supplier must achieve in order to safely meet the buyer's Cpk requirement, given the buyer's sample size, n.
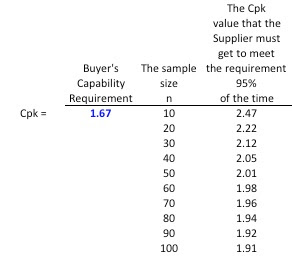
Table 2: Buyer's Requirement is a Cpk of 1.67